定义波德图是一种用于控制系统设计和分析的图形方法。在波德图中,使用对数尺度有助于简化用图形表示系统频率响应的方法。
对数标度的思想是由亨德里克•波德(george w . bush)。
在波德图中,幅值的对数和相角的对数分别表示频率的对数值。
需要预兆情节
在前面我们已经看到频率响应曲线的基本形式表示幅值和相位角之间的图形是不同的输入频率的值,即ω。在这样的图中,ω从有变化0到∞可以得到不同的幅值和相角值。然而,在线性尺度上容纳所有的幅值和相角值是相当困难的。
因此,H.W. Bode为控制系统的稳定性分析提出了一种不同但有效的方法。
什么是预兆情节?
正如我们最近讨论的那样极地的情节一个正常的线性比例被用来描绘的大小与相角的反应不同的值ω。但在波德图中,用对数比例尺代替常规的线性比例尺。
基本上,利用波德图,一个正弦传递函数的系统可以表示为两个独立的图。在这两幅图中,一幅图对应幅值与频率的关系,另一幅图对应系统相位角与频率响应的关系。
同时,两幅图上的所有3个参数都绘制了对数尺度的草图。
所以,更简单地说,我们可以说一个波德图由2个图组成:
1.级的阴谋在此图中,震级以对数值对频率的对数值表示。
对于传递函数G(jω)H(jω),为了用对数表示其大小,我们需要找到,![]()
这个幅度用dB表示为log10ω。这一点见下文所示的一般表示图:
2.相角情节在这里,以度数表示的相位角是根据频率的对数值绘制的。
这里,角值G(jω)的度数是对着对数画的10ω。图中为相角图的一般表示:
波德图也被称为对数图,因为它是在对数尺度上绘制的,并分别表示了幅度和相位角在频率方面的大范围变化。因此,波德图是在半对数坐标纸上绘制的。
此外,我们可以看到,在这两幅图中,频率的对数值在x轴上缩放,因此,x轴可以保持公共,幅值和相角图都可以在同一张对数纸上绘制。
需要指出的是,假设有系统G(jω)H(jω)的开环传递函数,我们必须利用开环系统的频率响应来确定闭环稳定性。然后,不仅仅是G(jω),而是G(jω)H(jω)的大小和相位角与对数相对应10ω。
开环传递函数标准因子的波德图
对于开环传递函数G(jω)H(jω),对于各相关因子,绘制波德图的过程如下:
- 改变给定的s域传递函数到频域通过替换s与jω。
- 确定大小,用下列公式表示为dB:
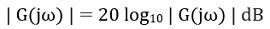
- 现在,确定相角φ,单位为:
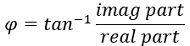
- 进一步,考虑必要的近似,绘制幅值和相角与对数ω的关系图,为ω在0到∞之间的不同值。
现在让我们分别讨论每一个因素。
1.系统增益,即K
如果
因此,以dB为单位的幅值可以表示为:![]()
在上述的绝对值方程中,由于常数K的存在,绝对值对于ω0到∞的每一个值都是恒定的。因此,在星等图中,它由一条平行于x轴的直线表示。
然而,对于K>1,直线将出现在0 dB参考线上方20 log K的距离处。而对于K<1,这条线将出现在参考线以下20 log K的距离处。
这意味着在大小方面;K的影响不表现出变化。所以20 logkdb对于所有频率都是常数。
因为,![]()
相角φ为:
因此,这表明,增益因子K对相位角图的贡献是0°。
因此,对于K的每一个正值,相图规格保持不变。但是,对于K的每一个负值,它将对图中的相位角贡献-180°对于K的每一个值0到∞。
2.原点的极点或零点
考虑原点处的单极,![]()
在复杂的形式,![]()
现在,计算大小,
以dB为单位的星等将表示为:
这可以写成:![]()
现在我们来检查ω的不同值的大小变化。
对于ω= 1,![]()
对于ω= 10,![]()
ω= 100,![]()
ω= 0。1,![]()
这里,我们将频率取为10的倍数,这表明变化为10。这表示这里的震级为-20分贝/十年。
此外,对于ω= 1,量级为0 dB,因此-20 dB的斜率将与参考线相交,即在ω= 1时0 dB。
在ω= 0.1和ω= 10时,其值分别为+ 20 dB和-20 dB。
根据这些数据,原点1极的星等图如下:
现在,计算相位角,![]()
这里,相位角与ω无关。因此,原点1极的相图就是平行于x轴的一条线。
所以,在这里我们已经给出了关于波德图的想法,在接下来的文章中我们将看到一些构造波德图的示例。
留下一个回复